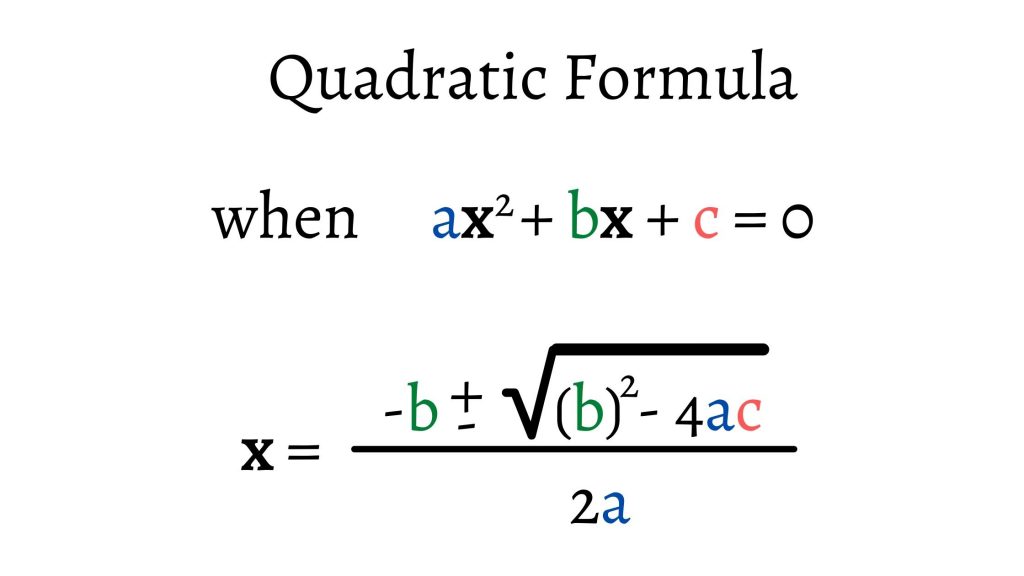Nice Tips About How To Write A Quadratic Function In Standard Form

Mario's math tutoring.
How to write a quadratic function in standard form. X^ {\msquare} \log_ {\msquare} \sqrt {\square} \nthroot [\msquare] {\square} \le. Thus, the general form of a quadratic equation is also of the form ax2+ bx + c = 0, where a ≠ 0. 33k views 3 years ago algebra 2.
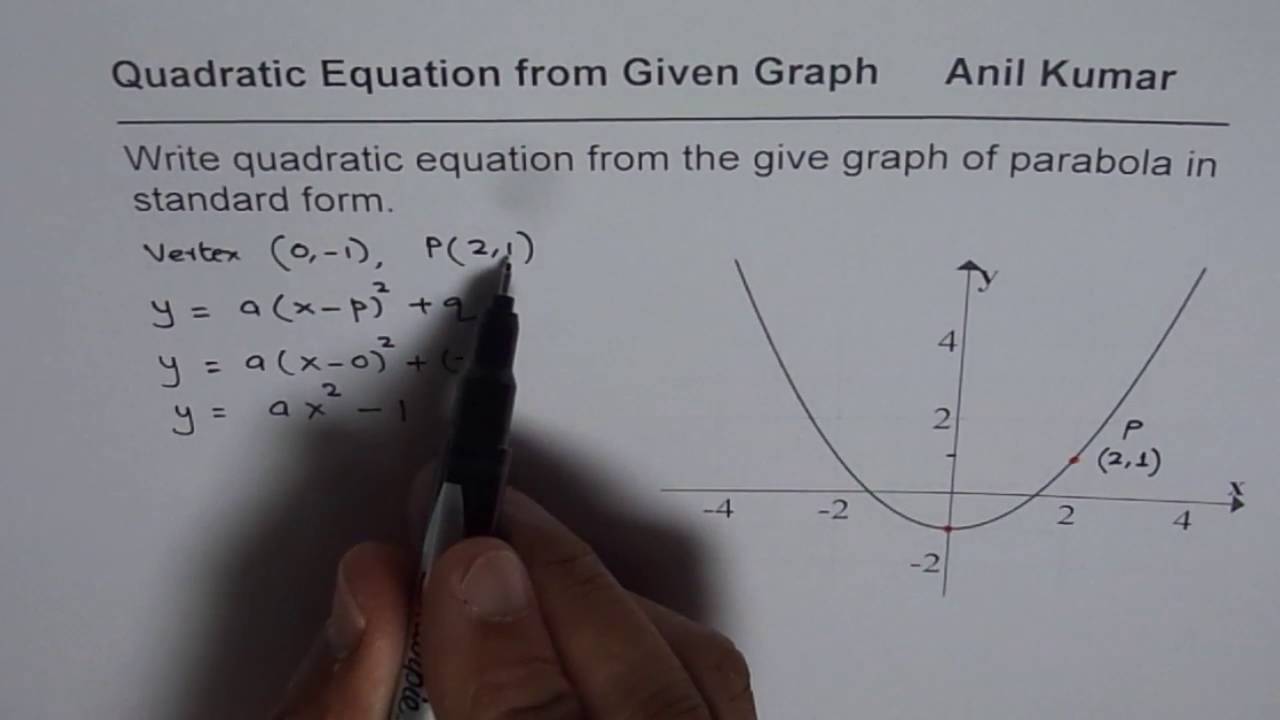
The general form of a quadratic function is f(x) = ax2 + bx + c with real number parameters a, b, and c and a ≠ 0. The quadratic formula gives solutions to the quadratic. How to write the equation of a quadratic function given its graph:
Learn how to graph any quadratic function that is given in standard form. The general form of a quadratic function presents the function in the form. The exploration is carried by changing the values of all 3.
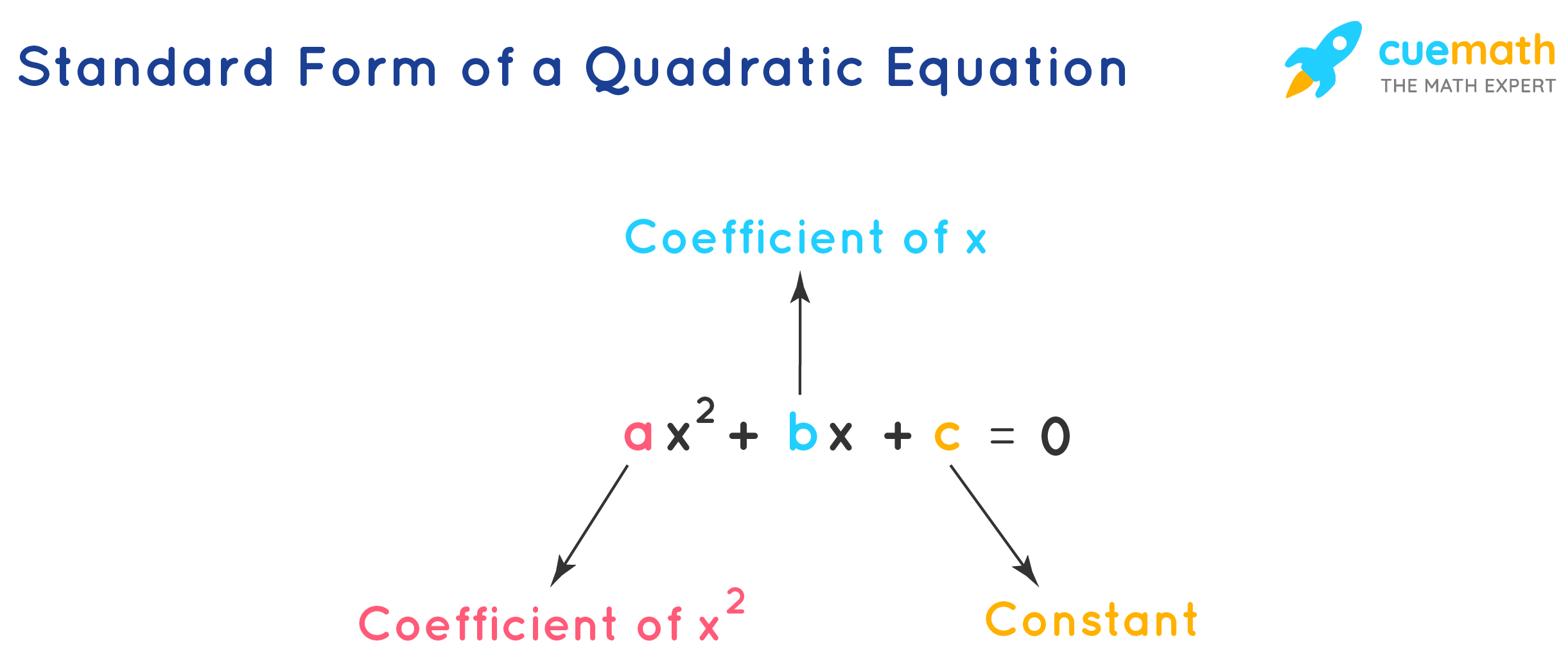
The standard form of a quadratic equation is also known as its general form. How to write quadratic equations in standard form. The graph of a quadratic function is a parabola.
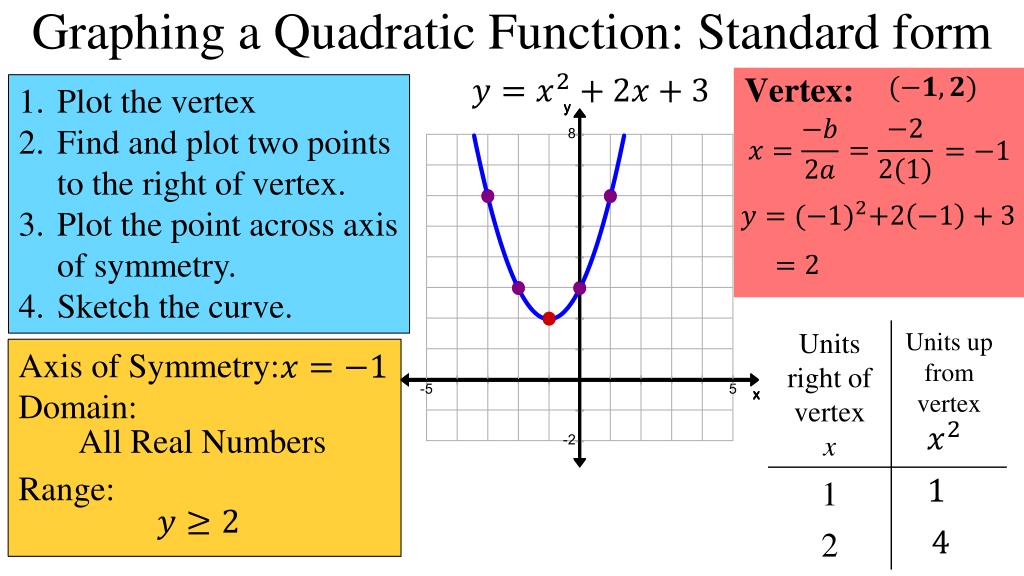
The graph of a quadratic function is u shaped and is called a parabola. Introduction to the quadratic equation | quadratic equations | algebra i | khan academy. Steps in writing a quadratic equation in standard form.
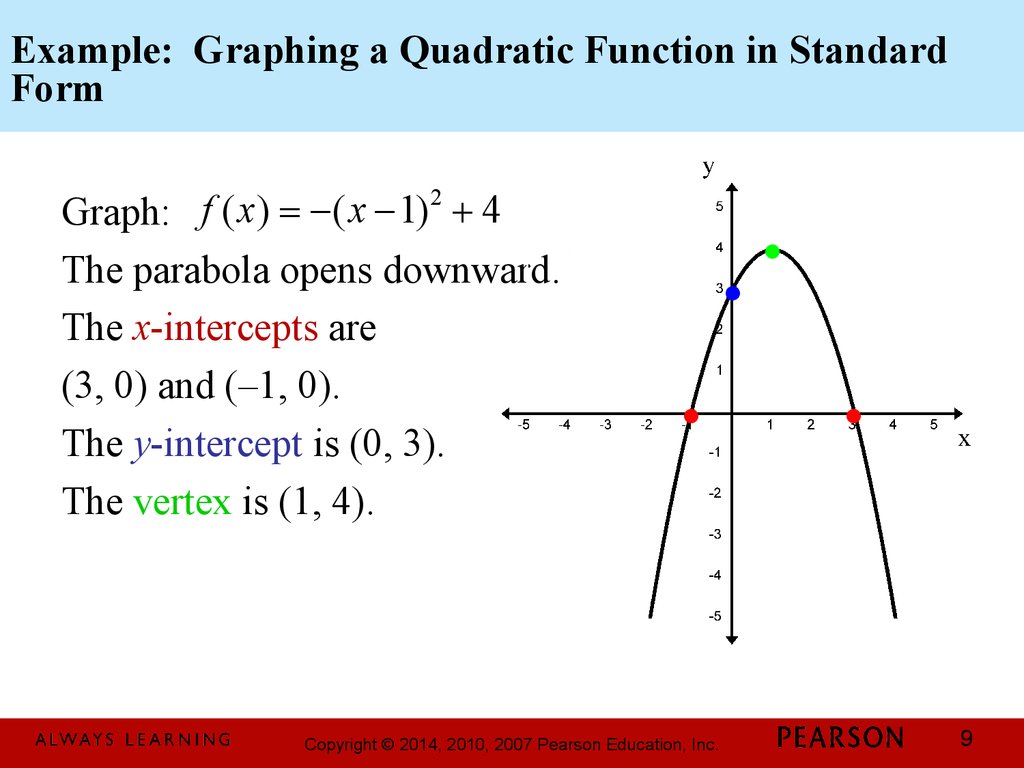
Write the equation for the quadratic function shown in the following graph in standard form. To write a quadratic equation in standard form, it’s crucial to understand its structure. , so here a = 1.
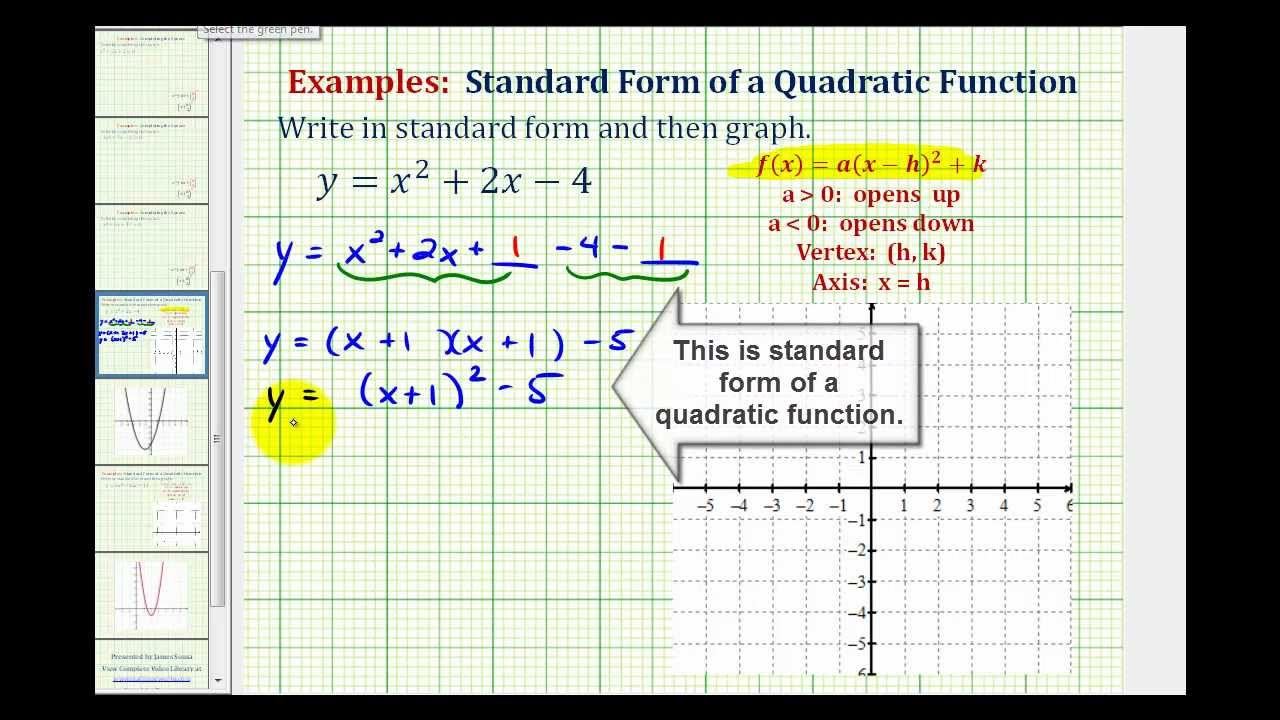
Now, for graphing quadratic functions using the standard form of the function, we can either convert the. Where a, b, and c are real numbers and a ≠ 0. This algebra video tutorial explains how to convert a quadratic equation from standard form to vertex form and from vertex form to standard form.
The general equation of a quadratic function is f (x) = ax 2 + bx + c. If a > 0, the parabola opens upward. To solve a quadratic equation, use the quadratic formula:
Besides writing a quadratic equation in standard. Y=ax^2+bx+c y = ax2 +bx+ c. F(x) = ax2 + bx + c.
Graph quadratics in standard form. X 2 + 4 x − 21 = 0. Quadratic functions in standard form.

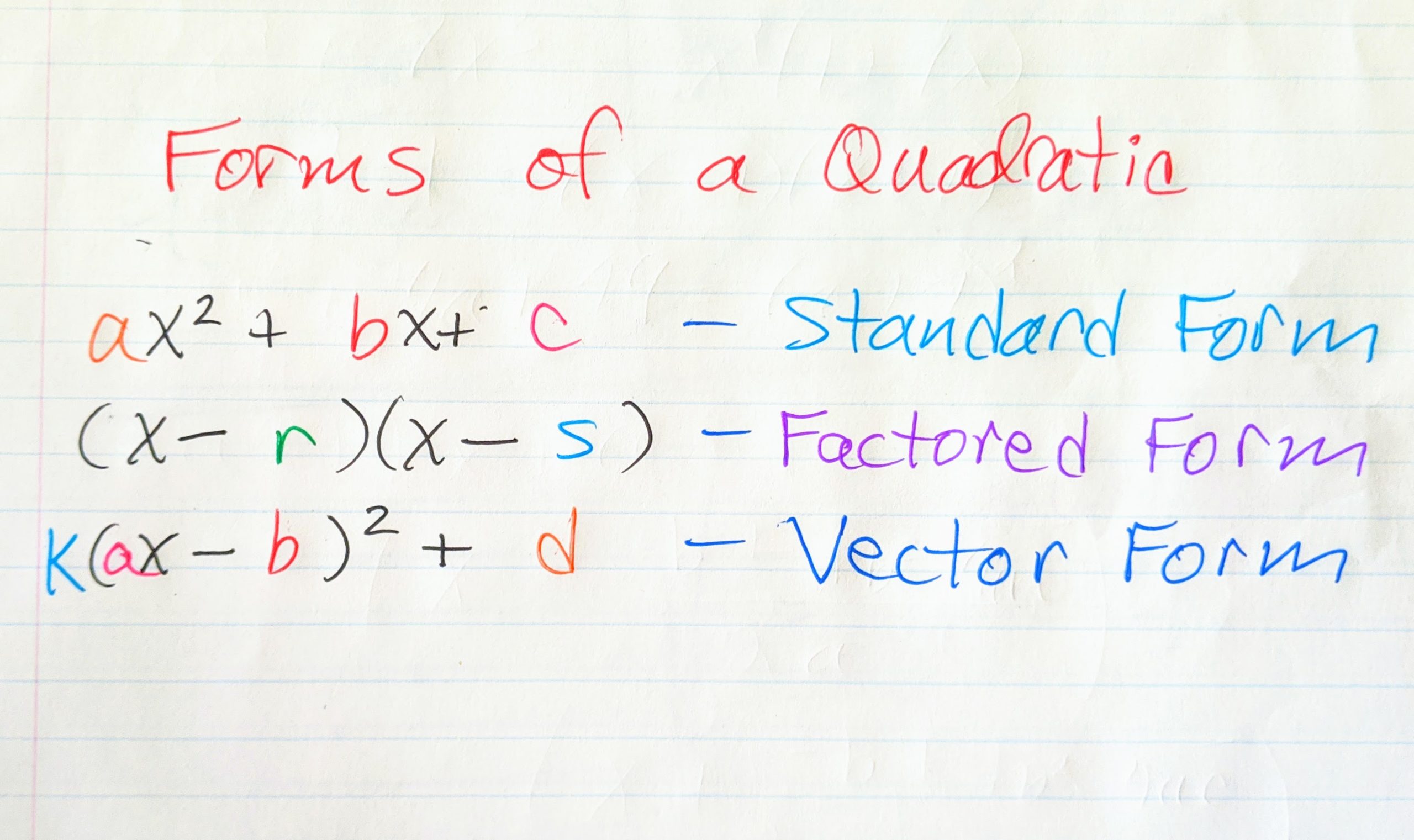



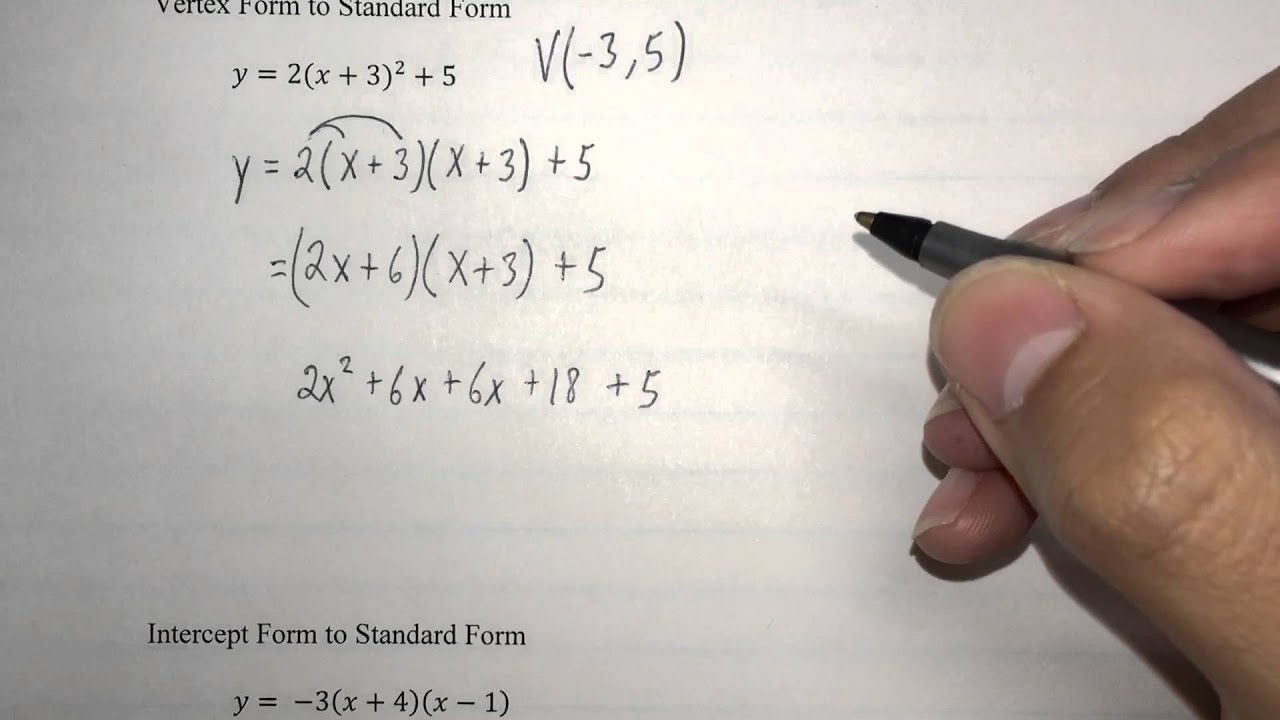


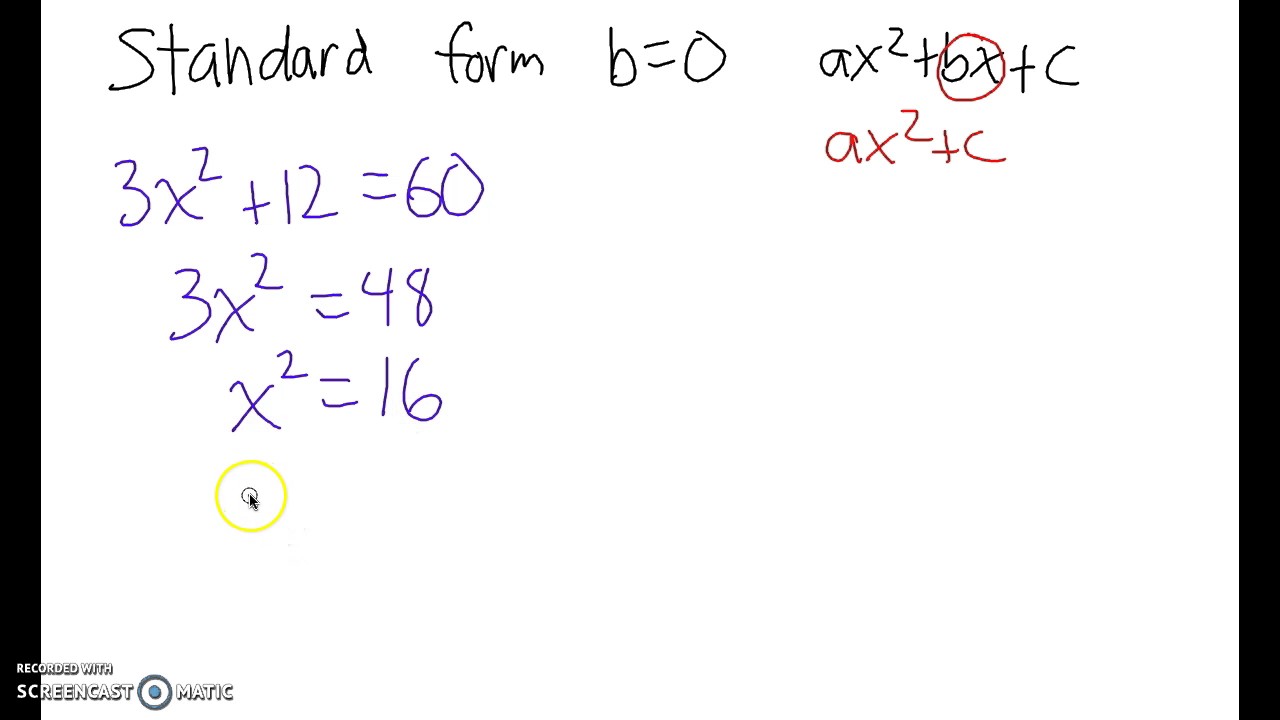
.PNG)